全连接层softmax原理详解与应用场景分析

全连接层与Softmax原理详解及应用场景分析

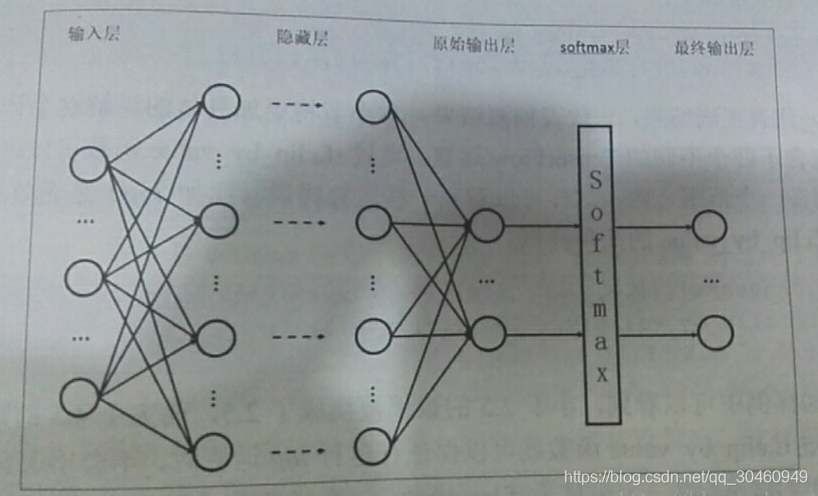
在深度学习网络中，全连接层（Fully Connected Layer）是一种基础的神经网络结构，其核心功能是将前一层的所有神经元与当前层的每个神经元建立全局连接。假设前一层的输出是维度为$n$的向量$X=[x_1, x_2, ..., x_n]$，全连接层通过权重矩阵$W$（维度为$m \

imes n$）和偏置向量$B=[b_1, b_2, ..., b_m]$，计算得到输出$Y = W \\cdot X + B$。这里的$m$代表当前层的神经元数量，每个神经元对应一个特征维度。全连接层通常搭配激活函数（如ReLU）使用，以增强非线性表达能力。

Softmax函数则是多分类任务中的核心组件，其数学表达式为：

$$

ext{Softmax}(y_i) = \\frac{e{y_i}}{\\sum_{j=1}k e{y_j}}

$$

它将全连接层的输出$y_1, y_2, ..., y_k$映射为概率分布，满足$\\sum_{i=1}k \

ext{Softmax}(y_i) = 1$。通过指数运算，Softmax会放大较大值的比重，同时抑制较小值的贡献。例如，若全连接层输出为$[3, 1, 0.5]$，经过Softmax处理后可能得到$[0.84, 0.11, 0.05]$，直观体现类别概率。

核心原理剖析

1. 全连接层的计算特性

2. Softmax的动态特性

应用场景与工程实践

1. 图像分类任务

2. 自然语言处理

3. 多模态模型

局限性及替代方案

总结

全连接层与Softmax的组合是深度学习中端到端分类建模的基石。其设计需权衡特征表达力与计算成本，在图像、文本、多模态等领域均有不可替代的价值。理解其数学本质及工程实现细节，是优化模型性能的关键。